Tyrone 的博客

什么是栈、栈的使用场景？

发表于 更新于 分类于
本文字数： 7.9k 阅读时长 ≈ 7 分钟
栈的特点和实现

如何理解栈？

关于”栈”，就像是一摞叠在一起的书籍。当我们放书籍的时候，都是一本本书的摞起来；当我们需要取书籍的时候，也是需要从上到下
一个个的依次的取。

所谓的栈：就是后进者先出，先进者后出，这就是典型的 栈 的结构。

从栈的操作特性上来看，栈是一种”操作受限”的线性表，只允许在一端插入和删除数据。

从功能上来说，数组和链表确实可以替代栈，但是特定的数据结构是对特定场景的抽象，而且，数组或者链表暴露了太多的操作接口，操作上的灵活，
在使用时也就会变得不可控，自然也就更容易出错。

当某个数据集合只涉及在一端插入和删除数据的时候，并且满足后进先出、先进先出的特性，这时我们就应该首选”栈”这种数据结构

如何实现一个”栈”？

栈可以使用数组来实现，也可以使用链表来实现；
这里我使用数组来实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Stack(object):
    def __init__(self):
        self._stack = []

    def push(self, data):
        self._stack.append(data)

    def pull(self):
        self._stack.pop()

    def top(self):
        return self._stack[-1]

    def size(self):
        return len(self._stack)

先说结论：
栈的空间复杂度为 O(1), 时间复杂度为 O(1)。
这里存储数据需要一个大小为 n 的数组，并不是说空间复杂度就是 O(n)。我们在判断一个空间复杂度的时候，是指除了原本的数据存储空间外，
算法运行还需要额外的存储空间。

对于时间复杂度来说，入栈和出栈都是 O(1)

栈在函数调用中的应用

函数调用栈

栈作为一个比较基础的数据结构，比较经典的应用场景就是函数调用栈。

操作系统给每个线程分配了一块独立的内存空间，这块内存被组织成栈这种数据结构，用来存储函数调用时的临时变量。

1
2
3
4
5
6
7
8
def main():
    a,b, c = 1,2, 3
    _res = add(a,b)
    res = _res + c
    return res

def add(a, b):
    return sum(a,b)

调用顺序：main() –> add()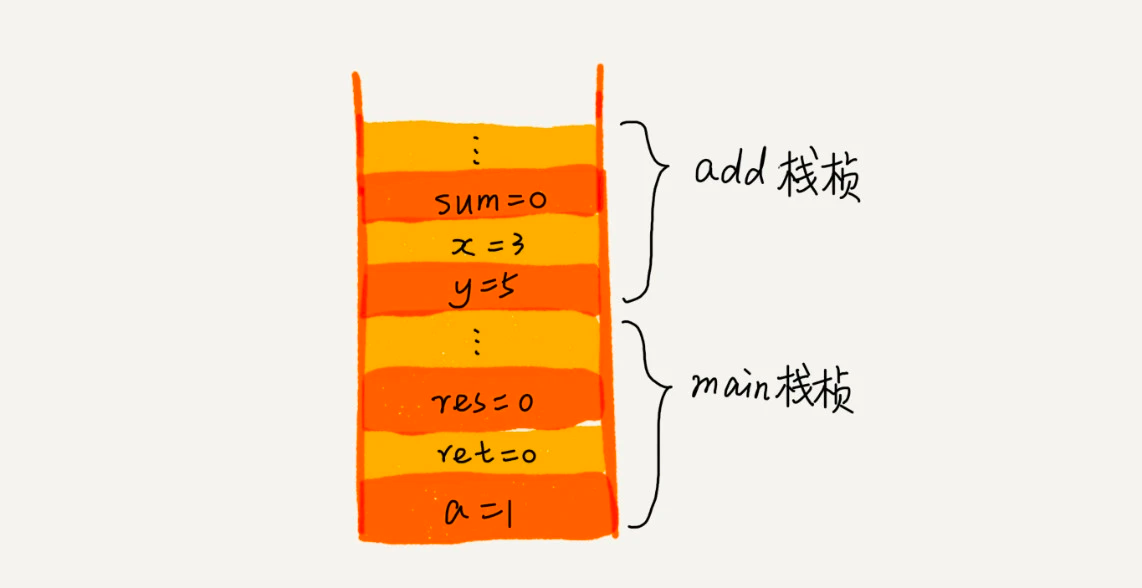
direct

表达式求值

四则运算的实现
例如：16+26*36-2/2

实现思路：

  1. 维护一个栈，然后
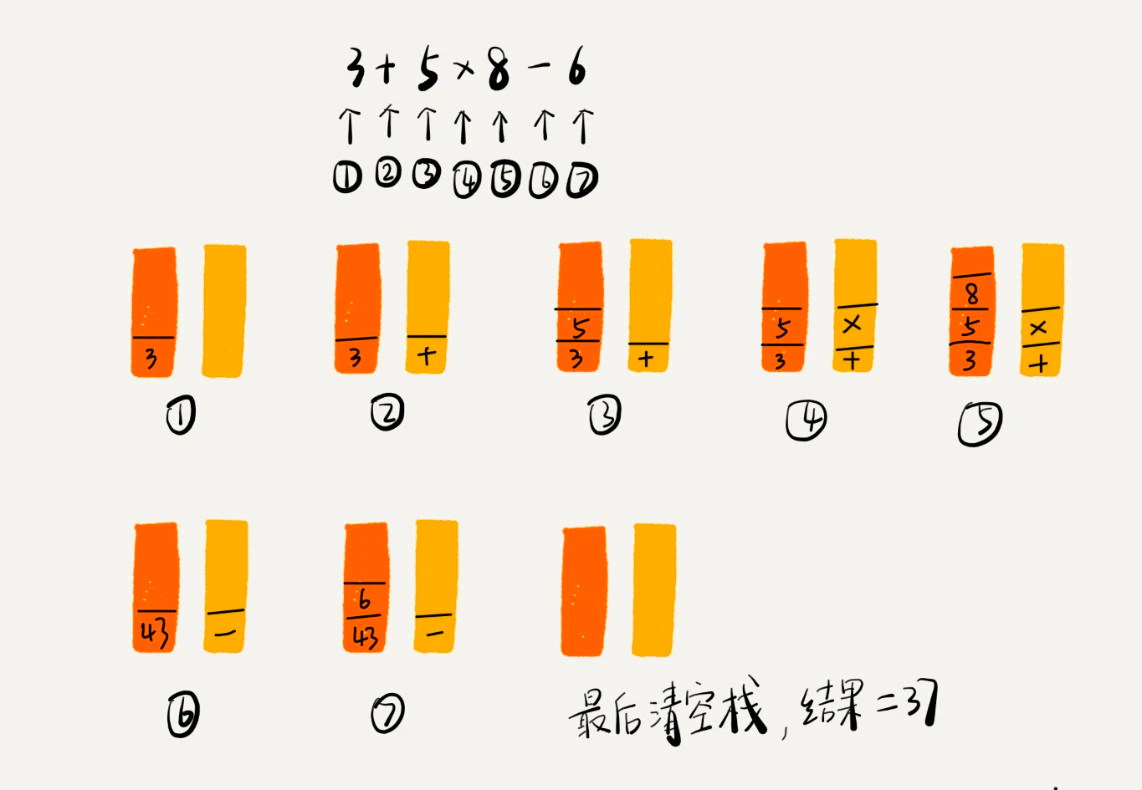
    img_2.png

实际上，编译器就是通过两个栈来实现的。其中一个来保存操作数的栈，另一个保存运算符的栈。

基本运算器实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def calculate(s: str) -> int:
    n = len(s)
    stack = []
    preSign = '+'
    num = 0
    for i in range(n):
        if s[i] != ' ' and s[i].isdigit():
            num = num * 10 + ord(s[i]) - ord('0')
            print(num)
        if i == n - 1 or s[i] in '+-*/':
            if preSign == '+':
                stack.append(num)
            elif preSign == '-':
                stack.append(-num)
            elif preSign == '*':
                stack.append(stack.pop() * num)
            else:
                stack.append(int(stack.pop() / num))
            preSign = s[i]
            num = 0
    return sum(stack)

浏览器前进和后退功能实现

解题思路：使用两个栈，A 和 B，将访问的页面一次压入栈 A 中，当点击后退按钮时，再依次从栈 A 中出栈，并将出栈的数据依次放入栈 B 中。点击前进按钮时，依次从栈 B
中取出数据，放入到 A 中。当栈 A 中没有数据时，那就是说明没有页面可以继续后退浏览了。当栈 B 中没有数据的时候，那就说明没有页面可以点击前进按钮浏览了。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Stack(object):
    def __init__(self):
        self._stack = []

    def push(self, data):
        self._stack.append(data)

    def pull(self):
        return self._stack.pop()

    def top(self):
        return self._stack[-1]

    def is_empty(self):
        return self._stack == []

    def size(self):
        return len(self._stack)


class Brower(object):
    def __init__(self):
        self.__forward_stack = Stack()
        self.__back_stack = Stack()

    def surf(self, web_site_url):
        print('surf the website:{}'.format(web_site_url))
        self.__forward_stack.push(web_site_url)

    def forward(self):
        if self.__back_stack.is_empty():
            return
        top = self.__back_stack.pull()
        self.__forward_stack.push(top)
        print('forward to the website: {}'.format(top))

    def back(self):
        if self.__forward_stack.is_empty():
            return
        top = self.__forward_stack.pull()
        self.__back_stack.push(top)
        print('back to the website: {}'.format(top))



if __name__ == '__main__':
    brower = Brower()
    brower.surf('www.1.com')
    brower.surf('www.2.com')
    brower.surf('www.3.com')
    brower.surf('www.4.com')

    brower.forward()
    brower.back()
    brower.back()
    brower.back()
    brower.back()
    brower.back()
    brower.forward()

总结

栈是一种操作受限的数据结构，只支持入栈和出栈操作。
可以通过数组或者链表来实现。
入栈、出栈的时间复杂度都是 O(1)。

问题

为什么函数调用要用栈来保存临时变量呢？

函数调用时，符合后进先出的特性，用栈这种数据结构来实现，是最符合的。

从调用函数进入被调用函数，比如：main –> add –> res 。变化的是作用域。所以从根本上，只要保证每进入一个新的函数，都是一个新的作用域都可以。
而要实现这个，用栈会非常方便。在进入被调用函数的时候，分配一段栈空间给这个函数的变量，在函数结束的时候，将栈顶复位，正好回到调用函数的作用域内。

在 JVM 内存管理中有个堆栈的概念 ？

内存中的堆栈和数据结构堆栈不是同一个概念，可以说内存中的堆栈是真实存在的物理区，数据结构中的堆栈是抽象的数据存储结构。
内存空间在逻辑上分为三部分：

  • 代码区
  • 静态数据区
  • 动态数据区
    • 栈区
    • 堆区

代码区：存储方法体的二进制代码。高级调度（作业调度）、中级调度（内存调度）、低级调度（进程调度）控制代码区执行代码的切换。
静态数据区：存储全局变量、静态变量、常量、常量包括 final 修饰的常量和 String 常量。系统自动分配和回收。

栈区：存储运行方法的形参、局部变量、返回值。由系统自动分配和回收
堆区：new 一个对象的引用或地址存储在栈区，指向该对象存储在堆区中的真实数据。

相关题目

有效的括号

20 - https://leetcode-cn.com/problems/valid-parentheses/
解题思路：

    1. 括号是成对出现的，则判断字符串 s 是否为偶数，否则返回 False;
    1. 遍历字符串，先将 左括号压入栈，匹配到右括号时，则判断栈顶是否匹配到，否则返回 False; 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      def isValid_bracket(brackets: str) -> bool:
          if len(brackets) % 2 == 1:
              return False

          pairs = {
              ')': '(',
              ']': '[',
              '}': '{'
          }
          
          stack = Stack()
          for ch in brackets:
              if ch in pairs:
                  if not stack or stack.top() != pairs[ch]:
                      return False
                  stack.pull()
              else:
                  stack.push(ch)
          return stack.is_empty()



      if __name__ == '__main__':
          print(isValid_bracket('([{}])'))

      最小栈

      解题思路：维护一个辅助栈，在入栈的时候，依次与辅助栈中的数据比较，采用 min(val, min_stack[-1]) 的方式入栈。pop 时，min_stack 也会 pop
      155 - https://leetcode-cn.com/problems/min-stack/
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      class MinStack:

          def __init__(self):
              self._stack = []
              self.min_stack = [math.inf] # 存储正无穷大


          def push(self, val: int) -> None:
              self._stack.append(val)
              self.min_stack.append(min(val, self.min_stack[-1]))

          def pop(self) -> None:
              self._stack.pop()
              self.min_stack.pop()

          def top(self) -> int:
              return self._stack[-1]


          def getMin(self) -> float:
              return self.min_stack[-1]

      用两个栈实现队列

      232 - https://leetcode-cn.com/problems/implement-queue-using-stacks/
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      42
      43
      44
      45
      class MyQueue:

          def __init__(self):
              """
              Initialize your data structure here.
              """
              self.s1 = []
              self.s2 = []
              self.front = None


          def push(self, x: int) -> None:
              """
              Push element x to the back of queue.
              """
              if not self.s1:
                  self.front = x
              self.s1.append(x)

          def pop(self) -> int:
              """
              Removes the element from in front of queue and returns that element.
              """
              if not self.s2:
                  while self.s1:
                      self.s2.append(self.s1.pop())
                  self.front = None
              return self.s2.pop()

          def peek(self) -> int:
              """
              Get the front element.
              """
              if self.s2:
                  return self.s2[-1]
              return self.front

          def empty(self) -> bool:
              """
              Returns whether the queue is empty.
              """
              if not self.s1 and not self.s2:
                  return True
              return False

      比较含退格的字符串

      844 - https://leetcode-cn.com/problems/backspace-string-compare/
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      class Solution:
          def backspaceCompare(self, s: str, t: str) -> bool:
              def judge(s: str) -> str:
                  ret = []
                  for value in s:
                      if value != '#':
                          ret.append(value)
                      elif ret:
                          ret.pop()

                  return ''.join(ret)

              return judge(s) == judge(t)

基本计算器实现

224 - https://leetcode-cn.com/problems/basic-calculator/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def calculate(s):
    res, num, sign = 0, 0, 1
    stack = []
    for ch in s:
        if ch.isdigit():
            num = num * 10 + int(ch)
        elif ch == '+' or ch == '-':
            res += sign * num
            num = 0
            sign = 1 if ch == '+' else -1
        elif ch == '(':
            stack.append(res)
            stack.append(sign)
            res = 0
            sign = 1
        elif ch == ')':
            res += sign * num
            num = 0
            res *= stack.pop()
            res += stack.pop()
    res += sign * num
    return res


if __name__ == '__main__':
    print(calculate('1+(1+2)-(1-1)+1'))

基本运算器 3

https://leetcode-cn.com/problems/basic-calculator-iii/
基本运算元素：

  • (
  • )
  • -
  • +
  • *
  • /

运算符优先级：

  • 2
    • / *
  • 1
    • + -
  • 0
    • ( )

解题思路：

双栈法

  • stack_num 存储数字
  • stack_opt 存储运算符

最小原子计算：

  1. stack_num 中 pop 出两个数 A, B
  2. stack_opt 中 pop 出一个操作符 opt
  3. 计算结果：res = B opt A
  4. 存储运算结果：stack_num.append(res)

字符串枚举：

  1. 空格，continue 下一个循环
  2. 数字
  • 单个数字
    stack_num.append()
  • 多位数字
    解析多位数字，append
  • ‘(‘
    直接进入 stack_opt 栈
  • ‘)’
    重复最小原子计算，直到 stack_opt 栈顶为 (。然后 stack_opt 栈 pop
  • 操作符(+,-,*,/)
    比较当前操作符与 栈顶操作符优先级，若前者大于后者，则进行最小原子计算操作。
    反之，则压入 stack_opt 栈中。

3.遍历完所有字符串后，判断 stack_opt 是否为空，重复执行最基本计算操作，直到为空。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# 基本运算器

# 最小原子计算器
class Solution:
    def cal(self, A, B, opt):
        if opt == '+':
            return int(A) + int(B)
        if opt == '-':
            return int(B) - int(A)
        if opt == '*':
            return int(B) * int(A)
        if opt == '/':
            return int(B) / int(A)

    def basic_cal(self, stack_num, stack_opt):
        opt = stack_opt.pop()
        A = stack_num.pop()
        B = stack_num.pop()
        res = self.cal(A, B, opt)
        stack_num.append(res)

    def calculate(self, s:str) -> int:
        # stack_num && stack_opt
        stack_num, stack_opt = [], []
        priority = {
            '(': 0,
            ')': 0,
            '+': 1,
            '-': 1,
            '*': 2,
            '/': 2,
        }
        length = len(s)
        i = 0
        while i < length:
            if i == " ":
                i += 1
                continue

            if '0' <= s[i] <= '9':
                start = i
                while i+1 < length and '0' <= s[i+1] <= '9':
                    i = i+1
                num = int(s[start: i+1])
                stack_num.append(num)
            elif s[i] == '(':
                stack_opt.append(s[i])
            elif s[i] == ')':
                while stack_opt[-1] != '(':
                    self.basic_cal(stack_num, stack_opt)
                stack_opt.pop()
            else:
                while stack_opt and priority[s[i]] <= priority[stack_opt[-1]]:
                    self.basic_cal(stack_num, stack_opt)
                stack_opt.append(s[i])

            i += 1

        # 进行全部计算
        while stack_opt:
            self.basic_cal(stack_num, stack_opt)
        val = stack_num[-1]
        return int(val)

-------------THANKS FOR READING-------------