Tyrone 的博客

为什么使用链表&&实现

发表于 更新于 分类于
本文字数： 8.7k 阅读时长 ≈ 8 分钟
链表的特点&&实现

引言

从一个经典的链表应用场景：LRU 缓存淘汰算法说开去。

缓存是为了解决高低速存储之间的差距而引入的技术。

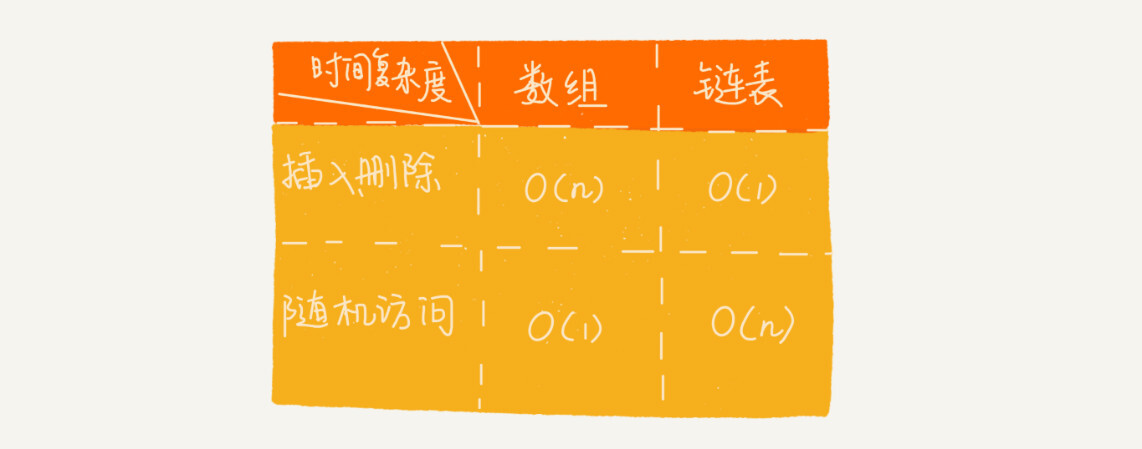
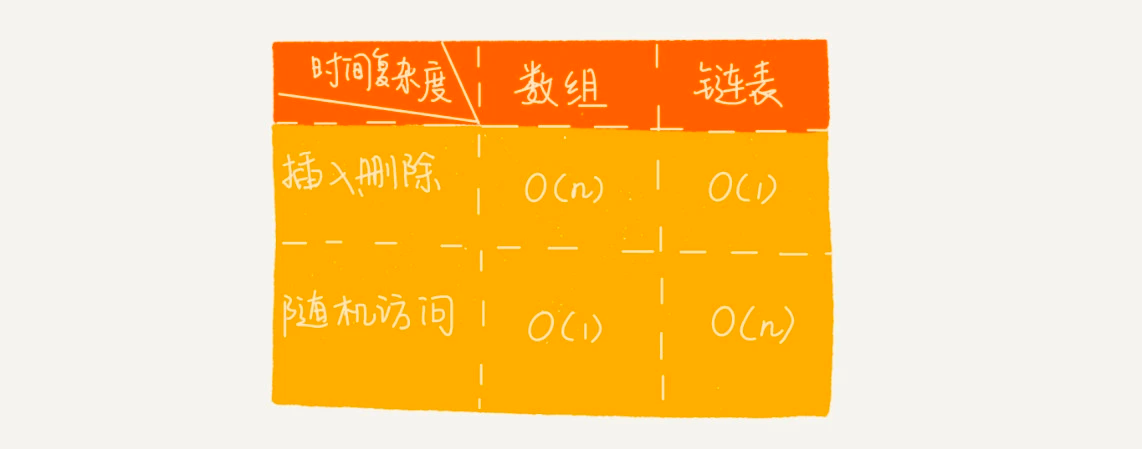
链表和数组对比：

img

缓存的大小有限，当缓存被打满的时候，就需要清理或者保留某些数据，这一部分就需要缓存淘汰策略来决定。

常见的策略有三种:

  • 先进先出策略 FIFO (First In, First Out)
  • 最少使用策略（Least Frequently Used）
  • 最近最少使用策略（Least Recently Used）

这些策略就和我们清理房间采取的策略一致

那么如何采用 链表，来实现 LRU缓存淘汰策略呢 ？

链表简介

首先解释一个 链表 的数据结构

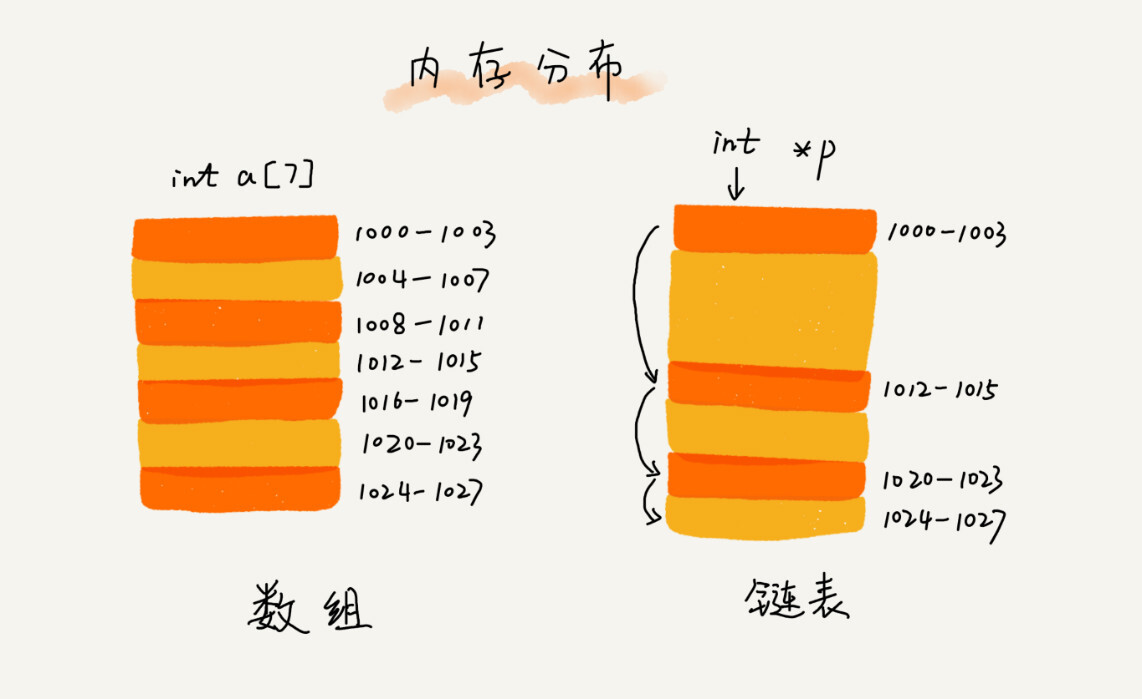
与数组结构不同的是，链表不需要连续的内存空间来存储，它是通过指针将一组零散的内存块串联起来使用。

用一张图直观的解释：

img

单链表

img

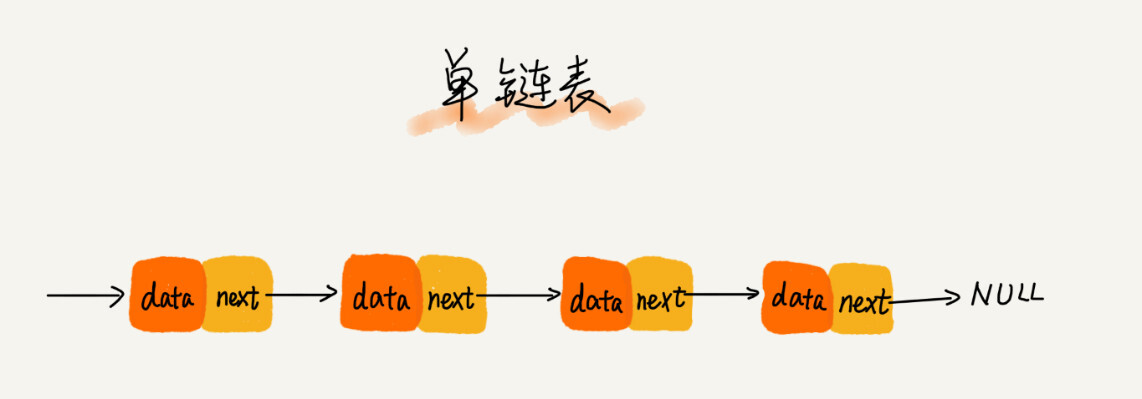
单链表是通过一个个节点（Node）组成的，每个节点包含了两个部分：

  • 存储数据的 data
  • 存储指针的next, 用于指向下一个 node

特点：

  • 数据的插入和删除非常迅速（无序）—— 时间复杂度 O(1)
  • 数据的查找时间复杂度是 O(n)

img

单链表的实现

  • 查找 - find()
  • 删除 - remove()
  • 链表元素添加
    • 头部添加元素 - add
    • 尾部添加元素 - append
    • 插入某个元素 - insert
  • 链表元素展示 - traverse()
  • 链表长度 - __len__
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
class Node(object):

    def __init__(self, data):
        self.data = data
        self.next = None


class LinkedList(object):
    """
    单链表的实现
    """

    def __init__(self):
        self.head = None

    def find(self, data):
        cur = self.head
        if cur is None:
            return -1

        while cur != None:
            cur_data = cur.data
            if cur_data == data:
                return True

            cur = cur.next

    def remove(self, data):
        cur = self.head
        pre = None
        if cur is None:
            return -1

        while cur != None:
            if cur.data == data:
                if cur == self.head:
                    self.head = self.head.next
                    return

                pre.next = cur.next
            pre = cur
            cur = cur.next

    def add(self, data):
        node = Node(data)
        node.next = self.head
        self.head = node

    def append(self, data):
        node = Node(data)
        cur = self.head
        if cur is None:
            self.head = node
            return
        while cur.next != None:
            cur = cur.next

        cur.next = node

    def insert(self, index, data):
        if index < 0:
            self.add(data)
        elif index > self.__len__():
            self.append(data)

        else:
            cur = self.head
            for i in range(index -1):
                cur = cur.next

            node = Node(data)
            node.next = cur.next
            cur.next = node

    def traverse(self):
        cur = self.head
        while cur != None:
            print(cur.data, end='-***-')
            cur = cur.next
        print()

    def __len__(self):
        count = 0
        cur = self.head
        while cur != None:
            count += 1

            cur = cur.next
        return count


if __name__ == '__main__':
    items = [1, 2, 3, 4, 5]
    chain = LinkedList()
    for value in items:
        node = Node(value)
        chain.append(value)

    chain.traverse()

    chain.append(6)

    chain.traverse()

    chain.remove(3)
    chain.remove(5)

    chain.traverse()
    chain.insert(1, 100)
    chain.traverse()
    print(chain.find(5), chain.find(1))

    print(len(chain))

循环链表

循环链表是一种特殊的单链表。它和单链表的唯一区别就是在尾节点。
循环链表的尾结点指针指向链表的头节点。

direct
这种数据结构比较适合处理具有环形结构特点的数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class CircleLink(SingleChain):
    def __init__(self):
        super(CircleLink, self).__init__()
        self._head = None

    def add(self, data):
        node = Node(data)
        if self._head is None:
            node.next = node
            self._head = node
        else:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            node.next = self._head
            self._head = node
            cur.next = node

    def append(self, data):
        node = Node(data)
        if self._head is None:
            node.next = self._head
            self._head = node
        else:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            node.next = self._head
            cur.next = node

    def travel(self):
        cur = self._head
        while cur.next != self._head:
            print("-**{}".format(cur.data), end='')
            cur = cur.next
        print("-**{}".format(cur.data), end='')  # 由于是 cur.next 判断的，故 cur 指向最后一个节点
        print()

    def find(self, data):
        if self._head is None:
            return False

        cur = self._head
        index = 0
        while cur.next != self._head:
            if cur.data == data:
                return index
            index += 1
            cur = cur.next
        if cur.data == data:  # 最后一个
            return self.__len__()

        return False

    def remove(self, data):
        cur = self._head
        if cur.next == self._head:
            self._head = None
            return

        pre = None
        while cur.next != self._head:
            if cur.data == data:
                pre.next = cur.next
                return
            pre = cur
            cur = cur.next

        # 退出循环, cur指向尾结点
        if cur.data == data:
            # 链表中只有一个结点
            pre.next = self._head
            return

    def __len__(self):
        count = 0
        cur = self._head
        while cur.next != self._head:
            count += 1
            cur = cur.next
        return count + 1  # 未计算最后一个 Node

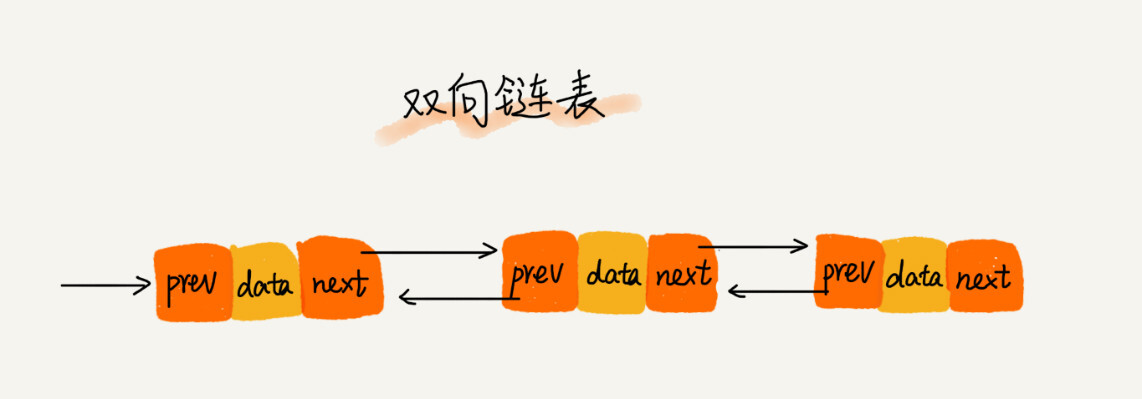
双向链表

双向链表，顾名思义，它支持两个方向，每个节点分为三个部分：

  • prev
  • data
  • next

双向链表可以支持 O(1) 时间复杂度的情况下找到前驱节点，双向链表在某些情况下的 插入、删除等操作都要比单链表简单、高效。

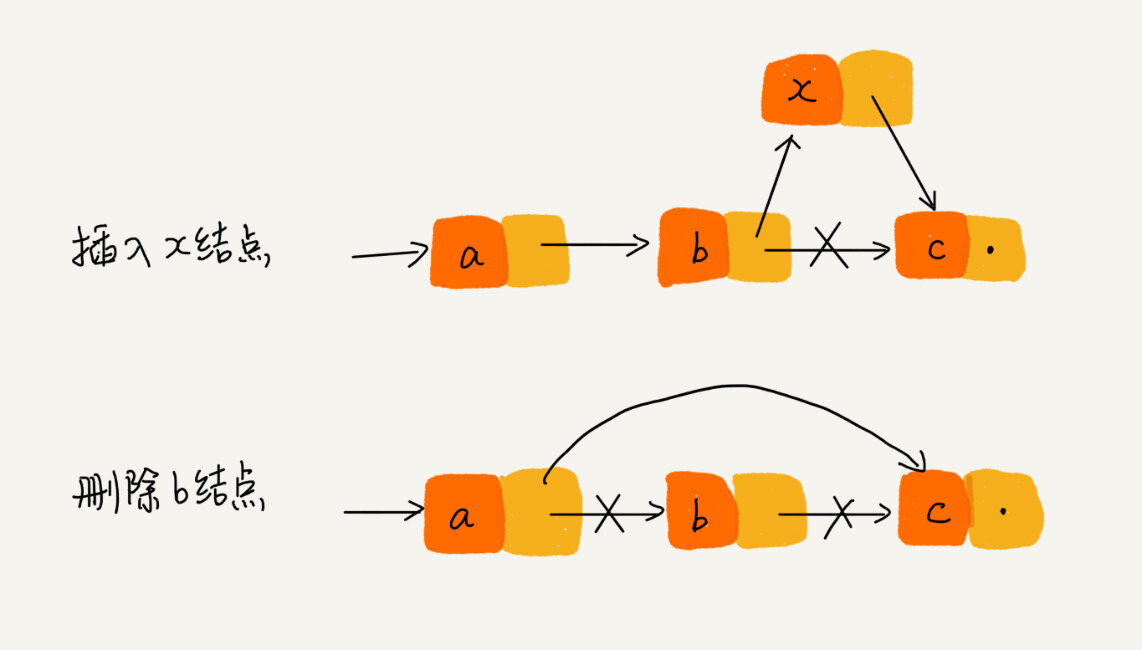
删除操作

  • 删除节点中“值等于某个给定值” 的节点

    对于这种情况，不管是单链表还是双链表，为了查找到值等于给定值的节点，都需要从头节点开始一个个依次遍历对比，找到后删除，时间复杂度为 O(n)

  • 删除给定指针指向的节点

    对于单链表来说，删除指定的节点时，还需要知道前驱节点，那么就会存在遍历的操作，时间复杂度为 O(n)。

    对于双向链表来说，是存在 prev 指针的，那么时间复杂度相对于是 O(1)

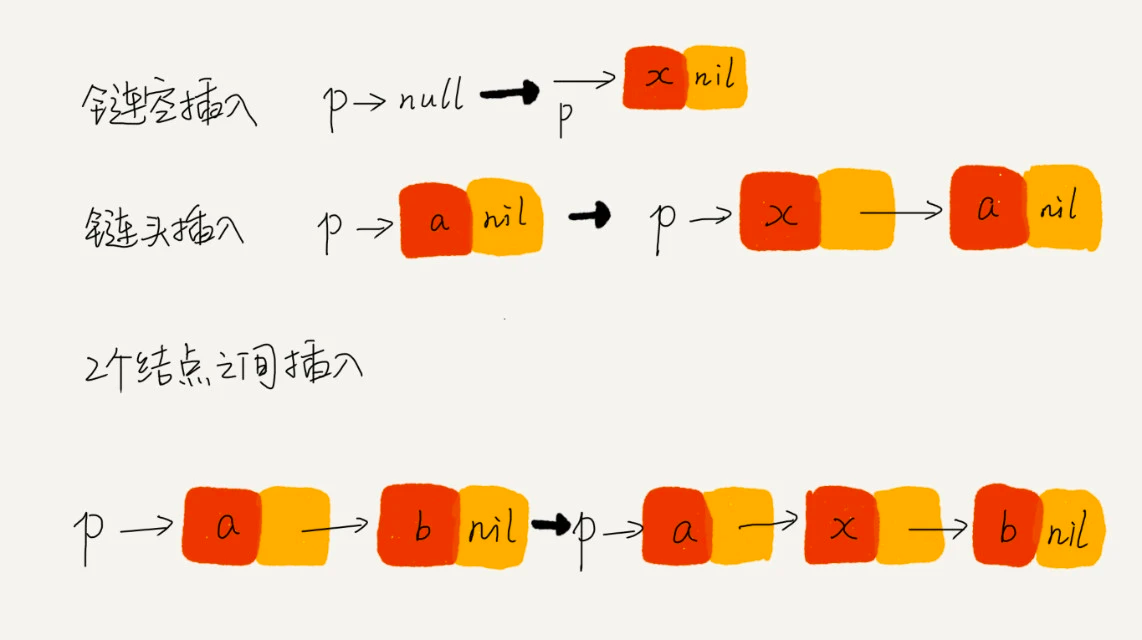
插入操作

  • 对于在某个节点前插入指定节点，时间复杂度是 O(1)

查询

对于一个有序链表来说，双向链表可以通过记录上次查找的位置 pos，根据要查找的值与 p 的大小关系，决定是往前还是往后查找，平均时间复杂度为 O(log(n))

img

双向链表实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
from chain.single_chain import SingleChain


# 双向链表
class XNode(object):
    def __init__(self, data):
        self.data = data
        self.prev = None
        self.next = None


# 双向链表
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Author: tyrone
File: 双向链表.py
Time: 2023/3/20
"""


class Node(object):
    def __init__(self, value):
        self.prev = None
        self.next = None
        self.value = value


class DoublyChain(object):
    def __init__(self):
        self.head = None
        self.length = 0
        self.history = (0, None)

    # append
    def append(self, value):
        cur = self.head
        node = Node(value)
        if cur is None:
            self.head = node
        else:
            # 找到最后一个节点
            while cur.next:
                cur = cur.next
            cur.next = node
            node.prev = cur

        self.length += 1

    # add
    def add(self, value):
        cur = self.head
        node = Node(value)
        if cur is None:
            self.head = node
        else:
            node.next = self.head
            self.head.prev = node
            self.head = node
        self.length += 1

    # insert
    def insert(self, index, value):
        if index <= 0:
            self.add(value)
        elif index > self.length - 1:
            self.append(value)
        else:
            cur = self.head
            count = 0
            while count < index:
                cur = cur.next
                count += 1

            node = Node(value)
            # 标记上一个
            prev = cur.prev
            # node.next = cur
            # node.prev = cur.prev
            # cur.prev.next = node
            # cur.prev = node

            prev = cur.prev
            prev.next = node
            node.prev = prev
            node.next = cur
            cur.prev = node


        self.length += 1

    # find
    def find(self, value):
        cur = self.head
        count = 0
        if cur is None:
            return -1
        else:
            while cur.next:
                cur = cur.next
                count += 1
                if cur.value == value:
                    return count

    def travel(self):
        cur = self.head
        while cur:
            print(cur.value)
            cur = cur.next


if __name__ == '__main__':
    double_chain = DoublyChain()
    double_chain.append(1)
    double_chain.append(2)
    double_chain.append(3)
    double_chain.insert(-1, -1)
    double_chain.insert(100, 100)
    double_chain.insert(2, 20000)
    double_chain.insert(4, 40000)

    cur = double_chain.head
    while cur:
        print(cur.value)
        cur = cur.next

    print(double_chain.find(40000))

总结

链表包括：

  • 单向链表
  • 双向链表
  • 循环链表

和数组相比，链表存储的数据是不连续的存储空间，数据之间采用指针引用方式连接。
链表各适合插入、删除操作频繁的场景，查询的时间复杂度较高。

链表实现注意点

  • 理解指针或引用含义

    将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针，或者反过来说，指针中存储了这个变量的内存地址，指向了这个变量，通过指针就能找到这个变量

  • 警惕指针丢失和内存泄露
    在插入指针的时候，注意操作的顺序，例如：

    1
    2
    p.next = x
    x.next = p.next

    上面的语句出现了自己指向自己的情况，交换两行就可以了
    删除链表节点的时候，也一定要记得手动释放内存空间。

  • 利用哨兵简化实现难度

    1
    cur = self.head

  • 重点留意边界条件处理

  1. 链表为空的时候
  2. 链表只包含一个节点的情况
  3. 链表只包含头尾节点
  • 举例绘图，辅助思考
    direct

思考题

LRU 的实现？

字符串是通过单链表来存储的，那如何判断一个回文字符呢？

解决思路：

法一：

使用快慢指针找到中点，然后将后半链表 reversed，然后一个指针在头部，一个指针在中部，逐个比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def is_palindrome(head) -> bool:
    if not head:
        return False

    if head.next == None:
        return True

    slow = reverse_node(find_middle_node(head))
    traverse(slow)
    traverse(head)
    while slow:
        if head.data != slow.data:
            return False
        slow = slow.next
        head = head.next
    return True

def find_middle_node(head):
    fast, slow = head, head
    while fast.next and fast.next.next:
        fast = fast.next.next
        slow = slow.next
    return slow


def reverse_node(head):
    p, rev = head, None

    while p:
        rev, rev.next, p = p, rev, p.next

    return rev

def traverse(node):
    cur = node
    while cur != None:
        print(cur.data, end='-***-')
        cur = cur.next
    print()


if __name__ == '__main__':
    my_str = "1012101"
    c = Chain()
    for v in my_str:
        c.append(v)

    print(is_palindrome(c.head))

链表练习题目

反转链表

206 - https://leetcode-cn.com/problems/reverse-linked-list/

解题思路：
p = p.next 循环， 将 head.next 的引用指向前一个节点即可

1
2
3
4
5
6
7
8
9
10
11
12
13
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        res, p = None, head

        while p:
            res, res.next, p = p, res, p.next

        return res

环状链表判断

解题思路：使用快慢指针，如果两个指针相遇了说明是环状链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:

        if head == None:
                return False

        i = head
        j = head

        while j != None and j.next != None:
            i = i.next
            j = j.next.next

            if i == j:
                return True

        return False

合并两个有序链表

21 - https://leetcode-cn.com/problems/merge-two-sorted-lists/

1
2
3
4
5
6
class Solution:
        def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
            if l1 and l2:
                if l1.val > l2.val: l1, l2 = l2, l1
                l1.next = self.mergeTwoLists(l1.next, l2)
            return l1 or l2

删除链表的到处第 N 个节点

19 - https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class ListNode:
    def __init__(self, val=0, next=None):
        self.data = data
        self.next = None

def removeNthFromEnd(head: ListNode, n: int) -> ListNode:
    def getLength(head: ListNode) -> int:
        length = 0
        while head:
            length += 1
            head = head.next
        return length

    dummy = ListNode(0, head)
    length = getLength(head)
    cur = dummy
    for i in range(1, length - n + 1):
        cur = cur.next
    cur.next = cur.next.next
    return dummy.next

876 - https://leetcode-cn.com/problems/middle-of-the-linked-list/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def middleNode(self, head: ListNode) -> ListNode:
        
        n, cur = 0, head
        while cur:
            n += 1
            cur = cur.next
        k, cur = 0, head
        while k < n // 2:
            k += 1
            cur = cur.next
        return cur

链表实现源码

https://github.com/tyronemaxi/algorithm/tree/main/chain

-------------THANKS FOR READING-------------