Tyrone 的博客

为什么 MySQL 索引采用 B+ 树实现？

发表于 更新于 分类于
本文字数： 2.3k 阅读时长 ≈ 2 分钟
MySQL B+ 树结构及来源

MySQL 索引的数据结构—— B+ 树

数据库索引是如何实现的？底层使用的是什么数据结构和算法呢？

对于数据来说，需要进行常用的一些查询操作，例如：

  • 根据某个值查找数据，比如 select * from user where id=1;
  • 根据区间查找数据，例如 select * from user where id > 1 and id < 10;
  • 排序，select * from user order by age;

还有一些非功能需求，例如：安全、性能、用户体验等等；

对于非功能性需求，我们着重考虑性能方面的需求：执行效率和存储；

对比常用的数据结构

  • 散列表

    散列表的查询性能很好，时间复杂度是 O(1)，但是散列表不能支持按照区间快速查找数据。

  • 平衡二叉树

    查询性能较高，时间复杂度为 O(logn)，但是仍然不足以支持按照区间快速查找数据

  • 跳表

    查询的时间复杂度为 O(logn)，并且跳表也支持按照区间快速地查找数据。我们只需要定位区间的起点值对应在链表中的节点，然后从这个节点开始，顺序遍历链表，直到结束。

根据分析，跳表是可以满足部分需求的。

实际上，数据库索引所使用到的数据结构和跳表非常相似，叫做 B+ 树。只不过它是通过二叉查找树演化过来的，而非跳表。

二叉树的改造——B+树过程

  • 支持范围查询

    子节点只存储索引，数据存储在叶子节点

  • 索引的存储问题

    • 时间换空间思想，存储在磁盘中

  • 减少了磁盘 IO

    • 使用多叉树，降低树的高度，减少磁盘 IO

  • 增/删数据的方法

    • 节点分裂/节点阈值管理

前面的分析可以知道二叉树的查找过程只能对单个数据的查找，并不能按照区间进行查找

我们可以对其进行改造：

树中的节点并不存储数据本身，而是只是作为索引。除此之外，我们把每个叶子结点串在一条链表上，链表中的数据是从大到小有序的。

img

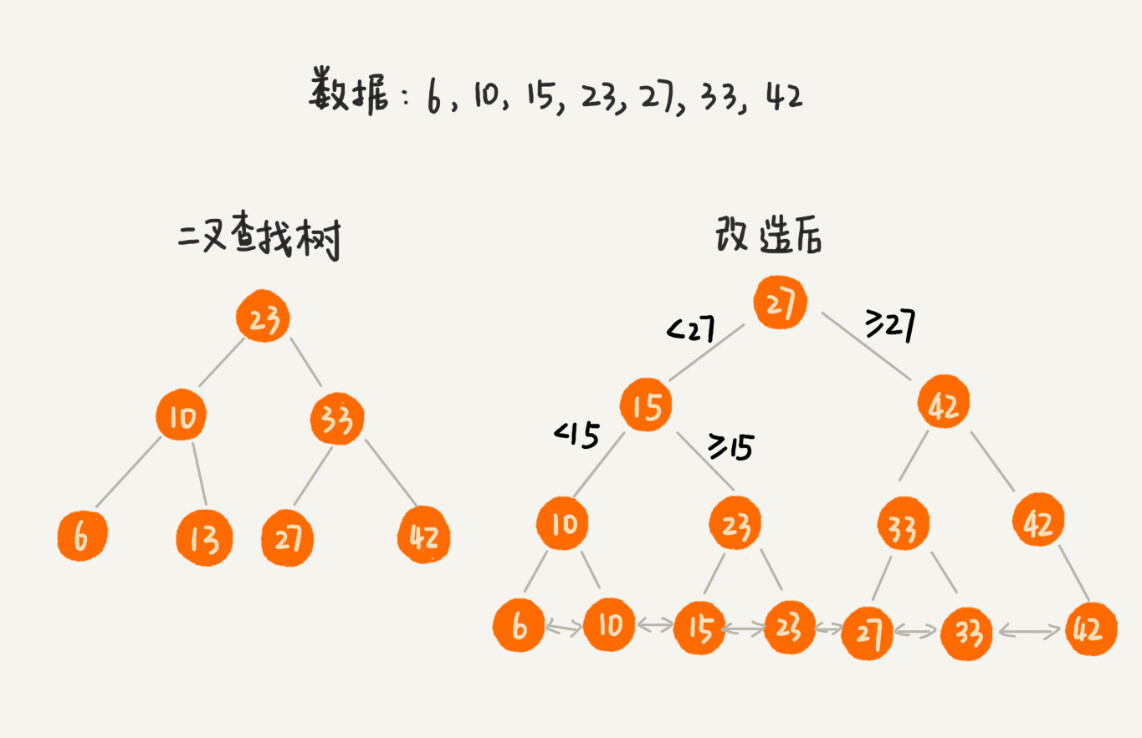
完成改造之后，如果我们要求某个区间的数据。我们只需要拿区间的起始值，在树中进行查找，当找到某个叶子节点之后，我们再顺着链表往后遍历。

但是当我们需要为几千万、上亿的数据构建索引，若在将索引存储在内存中，会占用大量的内存。

例如：

比如，我们给以一亿个数据构建二叉查找树索引，那么索引中的节点也大约是 1 亿个节点，每个节点假设占用 16 个字节，那就需要大约 1 GB 的内存空间，将这么大的数据存储在内存中是不可行的

例如使用时间换空间的思路，我们将索引存储在硬盘中，通常磁盘的访问速度是毫秒级别的，相比内存需要的时间是上万或者几十万倍。

二叉查找树，经过改造之后，支持区间查找了。当把索引存储在硬盘中时，每个节点的访问相当于一次 磁盘 IO 操作。树的高度就等于每次查询数据时磁盘 IO 操作的次数。

那么优化的关键时减少磁盘 IO 操作数，那么如何降低树的高度呢？
我们只需要将树的分叉增多，例如 5 叉树，10 叉树。

对于相同个树的数据构建 m 叉树索引，m 叉树中的 m 越大，那树的高度就越小，那 m 叉树中的 m 是不是越大越好呢？多大才是合适的。

不管是内存中的数据，还是磁盘中的数据，操作系统都是按页（一页大小通常是 4 KB），这个值可以通过 getconfig PAGE_SIZE 命令查看）来读取的，一次会读取一页的数据，当读取的数据量超过一页时，就会触发多次 IO 操作。所以，当我们在选择 m 大小的时候，要尽量让每个节点的大小等于一个页的大小。读取一个节点，只需要一次磁盘 IO 操作

img

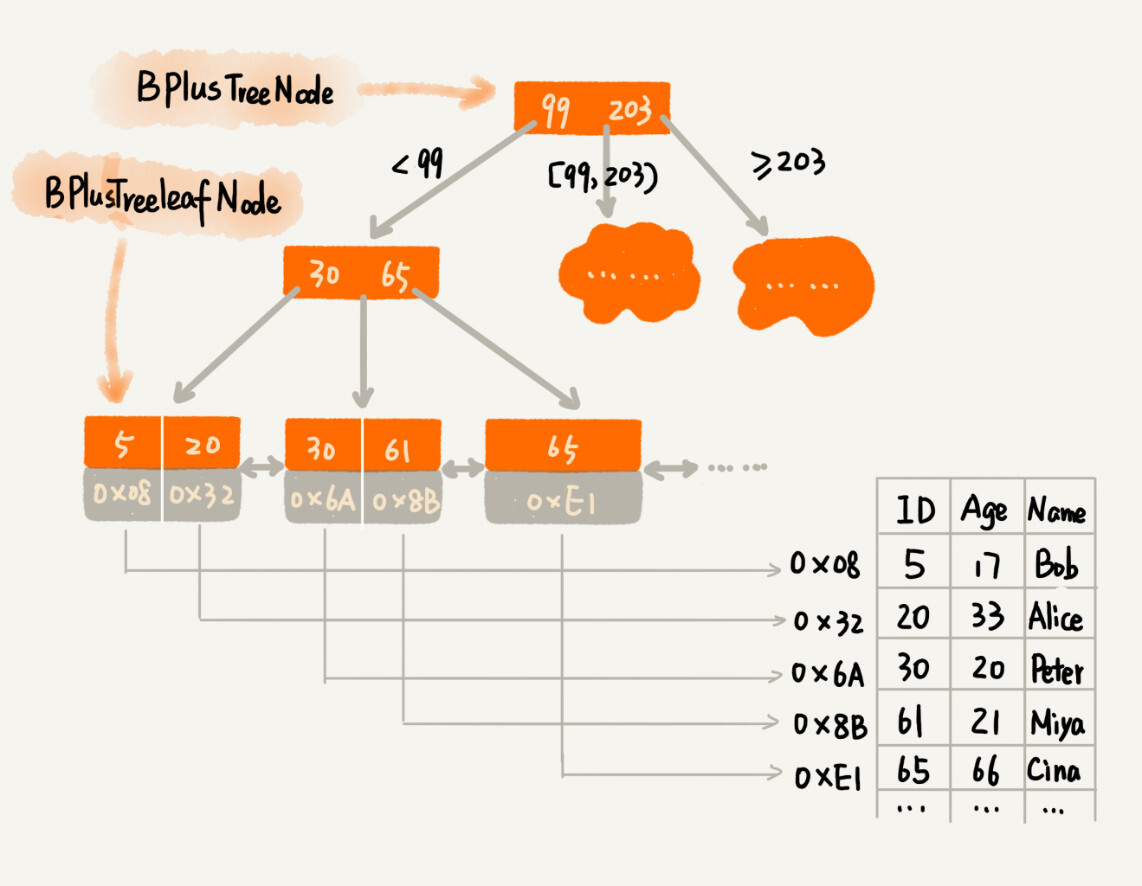
虽然索引可以提高数据库的查询效率，但是写入操作会变慢，这是因为：数据的写入过程，会涉及索引的更新，这是索引导致写入变慢的主要原因

数据写入的节点更新

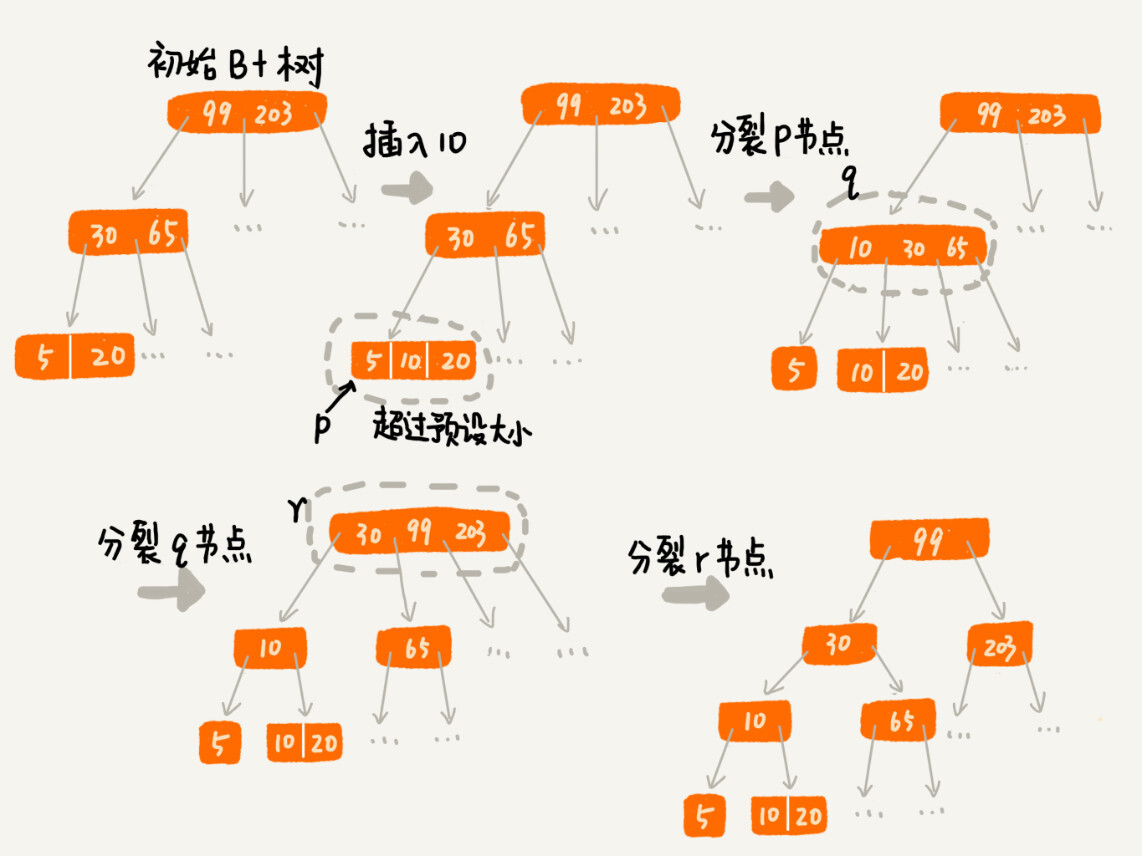
对于一个 B+ 树来说，m 值是根据页的大小事先计算好的。每个节点最多只能有 m 个子节点。在数据写入过程中，这样就有可能使索引中某些节点的子节点个数超过 m，这个节点的大小超过了一个页的大小。如何解决该问题呢？

当一个数据插入的时候，该页如果已经满了，我们只需要将这个节点分裂成两个节点。但是父节点为了为该节点建立索引，也会出现节点溢出情况，同样，我们也可以将该父节点分裂，采用这种级联反应，一直影响到根节点。

img

数据的删除

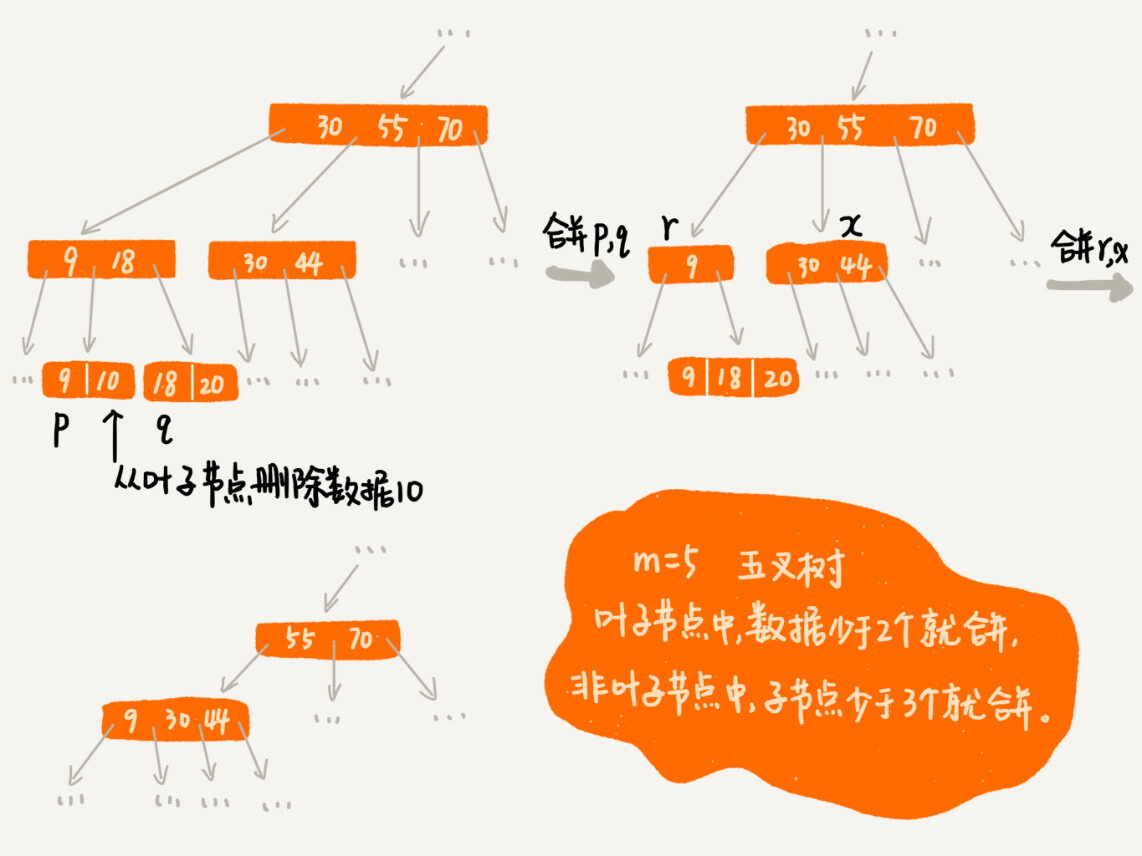
我们在删除某个数据的时候，也要对应地更新索引节点。这个处理思路有点类似跳表中删除数据的处理思路。频繁的数据删除，就会导致某些节点中，子节点的个数变得非常少，长此以往，如果每个节点的子节点都比较少，势必会影响索引的效率。

对于这种情况，我们可以设置一个阈值。在 B+ 树中，这个阈值等于 m/2。如果这个节点的子节点个数小于 m/2，我们就将它和相邻的兄弟节点合并。不过，合并之后节点的子节点个数有可能会超过 m。针对这种情况，可以进行分裂。

img

索引的深度问题

mysql 深度问题一般从 B+ 树的结构和数据库大小去分析，索引字段占内存大小，指针占内存大小（6Byte）

  • B+ 树非叶子节点存放的都是 key+nest 指针。叶子节点存放数据。
  • 非叶子节点键值数=子节点数
1
2
3
SHOW VARIABLES LIKE 'innodb_page_size'
--> 
16384;

mysql 索引中索引页默认大小 16 k；

假设 主键 id 为 bigint 类型：8 bytes

指针大小：6 bytes

已知，B+ 树子节点只存储指针，叶子节点存储数据。

16384/（8+6）= 1170

于是，对于每页来说，可以存储 1170 条数据；

  • 则 B+ 树深度和数据库数量的关系：

​ 1170 ** （n-1）* 16

  • 深度为 3 ：

​ 1170 *1170 *16 = 21902400（2千万数据）

所以一般数据库b+深度也就 3-5 层

参考

https://blog.csdn.net/styhm/article/details/109512895

https://time.geekbang.org/column/article/77830

-------------THANKS FOR READING-------------