什么是二分查找？

二分查找（Binary Search）算法，也叫做折半查找算法

二分思想

典型的猜数游戏，随机在 0-99 中选中一个数让人去猜，猜的过程中，每猜一次，就会告诉对方大了还是小了，直到猜中为止。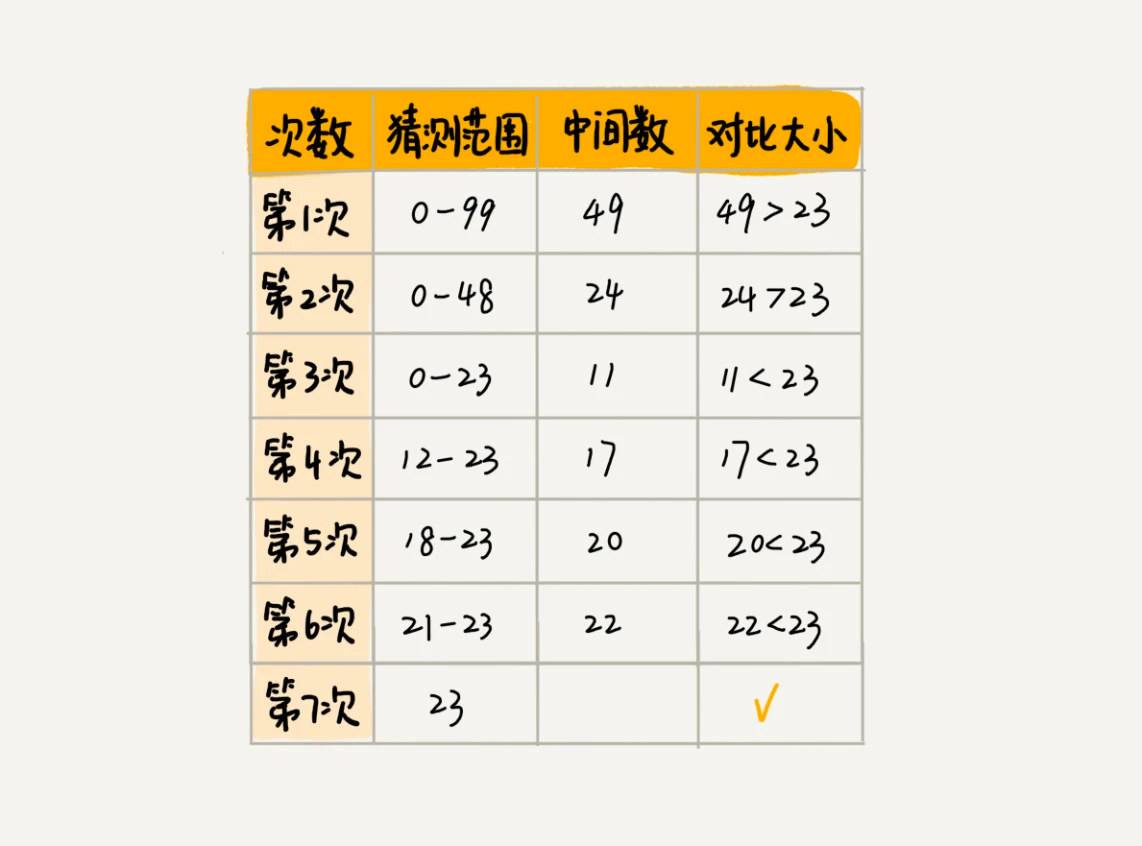

在这个游戏中，7 次就猜出来了。
如果是 0 - 999 的数字，最多也就要 10 次就能猜中。

二分查找针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0

二分查找的时间复杂度

二分查找是一种非常高效的查找算法，**时间复杂度为 O(logn)。
被查找区间的大小变化为：n, n/2, n/4, n/8, ……, n/2^k ……
已知通过 n/2^k=1 得到 k=log2n。所以时间复杂度就为：O(logn)

logn 是一个非常恐怖的数量级，即便 n 非常非常大，对应的 logn 也很小。2^32 次大约是 42 亿，但是利用二分查找，最多需要比较 32 次。

二分查找的递归与非递归实现

非递归

def binary_search(arr: list, guess: int):
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = low + ((high - low) >> 1)
        if arr[mid] < guess:
            low = mid + 1
        elif arr[mid] > guess:
            high = mid - 1
        else:
            return mid


if __name__ == '__main__':
    arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    index = binary_search(arr, 9)
    print(index)

三个注意点：

循环退出条件
low <= high，而不是 low < high
mid 取值
实际上，mid=(low+high)/2 的写法是有问题的。如果 low 和 high 比较大的话，两者之和就会溢出。
改进的方法是将 mid 的计算方式写成 low+(high-low)/2。
性能优化到极致的话，可以改写成位运算low+((high-low)>>1)。
low 和 high 的更新
low=mid+1 和 high=mid-1。如果直接写成 low=mid 或者 high=mid，就可能发生死循环。

递归实现

def half_search(arr, key, left, right):
    if left > right:
        return None
    mid = (left + (right - left) >> 1)
    if key == arr[mid]:
        return mid
    elif key > arr[mid]:
        return half_search(arr, key, mid + 1, right)
    else:
        return half_search(arr, key, left, mid - 1)

二分查找应用场景的局限性

在以上的分析中，二分查找的时间复杂度为 O(logn)，查找数据的效率非常高。

二分查找依赖的是顺序表结构，简单点说就是数组
二分查找针对的是有序数组
数据量过小或者过大也不适合二分查找

二分查找的变形问题

查找第一个值等于给定值的元素

# 查找第一个给定值
def first_search(arr, value):
    left = 0
    right = len(arr) - 1
    while left <= right:
        mid = (left + (right - left) >> 1)
        if arr[mid] > value:
            right = mid - 1
        elif arr[mid] < value:
            left = mid + 1
        else:
            if mid == 0 or arr[mid-1] != value:  # 若为 arr 的第一个元素或者前一个数不是 value
                return mid
            else:
                right = mid - 1  # 前移

    return -1

以上的代码中还是分为三种情况，即=,>,<,但是当 = 的时候，为了找到是列表中第一个找到的元素，需要向前比较，当前一个数不等于目标值时，则为第一个

查找最后一个值等于给定值的元素

def final_search(arr, value):
    left = 0
    right = len(arr) - 1
    while left <= right:
        mid = (left + (right - left) >> 1)
        if arr[mid] > value:
            right = mid - 1
        elif arr[mid] < value:
            left = mid + 1
        else:
            if mid == len(arr) - 1 or arr[mid+1] != value:  # 若为 arr 的最后一个元素或者后一个数不是 value
                return mid
            else:
                left = mid + 1  # 后移

    return -1

查找第一个大于等于给定值的元素

# 查找第一个大于等于给定值的元素
def first_greater_search(arr, value):
    left = 0
    right = len(arr) - 1
    while left <= right:
        mid = (left + (right - left) >> 1)
        if arr[mid] >= value:
            if mid == 0 or arr[mid - 1] < value:
                return mid
            else:
                right = mid - 1
        else:
            left = mid + 1

如果 a[mid] 小于我们要查找的值 value, 那要查找的值肯定在 [mid+1, right] 之间，所以 left = mid + 1
对于 a[mid] 大于等于给定着 value 的情况，判断是否是第一个大于等于给定值的情况：mid=0 或者前一个数小于要查找的值。

查找最后一个小于等于给定值的元素

def first_greater_search(arr, value):
    left = 0
    right = len(arr) - 1
    while left <= right:
        mid = (left + (right - left) >> 1)
        if arr[mid] > value:
            right = mid - 1     
        else:
            if mid == len(arr) - 1 or arr[mid + 1] > value:
                return mid
    
    return -1

问题思考

如何在 1000 W 个整数中快速查找某个整数？

如果我们内存限制是 100 MB,每个数据的大小是 8 字节，最简单的办法就是将数据存储在数组中，内存占用差不多是 80 MB,符合内存的限制。
可以先对这 1000 W 的数据从小到大排序，然后再利用二分查找随发，就可以快速地查找想要的数据了。

Tyrone 的博客

如何玩转二分法查找？